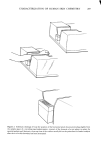
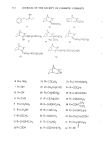
VISCOELASTIC MEASUREMENT ON FOAM 241 k, modulus of elasticity of spring M, mass 3', modulus of I I r/, modulus of elasticity I viscosity of of foam foam Figure 4. Mechanical model corresponding to the measurement by the apparatus where M is the mass of mechanical system, k is the modulus of elasticity of the coil spring, K is the elastance of foam, R is its resistance and x is an axial displacement. There are three cases of the solution for eq [1]. {(K + k)/M)1/5• Ae_•T t + Be_O• t [2] (a) R/2M X • (b) R/2M = X m (c) R/2M {(K + k)/M} e -m/2M (Ct + D) [3] {(K + k)/M} 1//'2 [4] x = Ee -m/2M sin {t •/'(K + k)/M - R2/4M 2 + q} where OZl, oz2, A, B, C, D and E are positive constants, t is time and q is phase dif- ference. A damped sinusoidal motion can be defined both the period of the oscillation Tu and the logarithmic decrement 8T are provided. Td and 8T are defined as eqs [5] and [6], respectively. Td = 2•r/{(K + k)/M- R•/4M =} [5] 8T = RTd/2M [6] From eqs [5] and [6], therefore, the elastance K and the resistance R of foam can be ob- tained experimentally. Provided the shape factor of the apparatus is represented by S, the modulus of elasticity •/and the modulus of viscosity •/of foam can be written as •/=SK = SM {4rr 2 (1/Td 2 - 1/T 2) + 8T2/Td 2} [7] = Sk {(1 + 8v2/4rr 2) T2/Td 2 - 1}

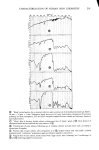
242 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS •1 = SR = SM (287/Td) [8] = Sk (8•/2•r 2) (T2/Td) where T is the period of free oscillation and is given by T = 2•' %/•/k [9] M and k were determined from eq [9] by measuring T at various weights. The shape factor S was calculated from eq [8] by using the experimental values obtained on a stan- dard viscosity sample (Showa Petroleum Co., JS 2000). We should point out that such an indirect determination of S involves the risk of allow- ing an error in measurement. The. reason for having to adopt the indirect way to de- termine S can be summarized as follows. A large volume of foam sample was required for the measurement in order to satisfy the condition of the flow between parallel plates under which S is theoretically obtained, since foam is generally a coarse disperse system. On the other hand, if such a large volume of foam is used in measurement, it is unavoidable that the foam becomes more heterogeneous in film thickness because of drainage in the film. This problem is expected to be solved by devising an entirely new type foam-generator providing a homogeneous foam to a measuring vessel where the condition of the flow between parallel plates is taken into consideration it is an im- portant subject for further study. 1200 1000 800 600 400 200 o : elasticity 70 ppm 70øC --- 40øC ß : viscosity 1.5 hours ( ]: specific volume 6.2 cc/min ] 0•000 rpm (10.5] • [8.9] -.o.... (8.2) -30 -20 o_ ,,,i,- -10 u • I • • • 0 O0 1 2 3 4 5 soap concentration, % wt/wt Figure 5. Dependence of the viscoelasticity of the foam on the toilet soap concentration. The specific volume of the foam sample is designated in brackets