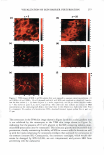
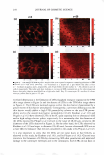
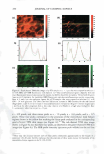
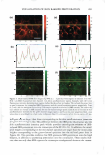
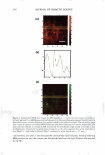
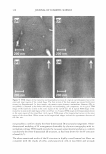
VISUALIZATION OF SKIN BARRIER PERTURBATION 271 which SRB may penetrate into the lipid bilayers of the SC. Conversely, as the peak height decreases and the peak width increases, there is more SRB present inside the corneocytes relative to the intercellular lipid bilayers. This serves as a qualitative indi­ cator of mechanism (a), that is, keratin denaturation in the corneocytes, because a disruption of the corneocyte envelope and subsequent keratin denaturation induced by the surfactant-humectant system should result in an increase in SRB penetration into the corneocytes in the SC. THEORETICAL DETERMINATION OF ENHANCEMENTS IN AQUEOUS PORE CHARACTERISTICS INDUCED BY SURFACTANT-HUMECTANT SYSTEMS USING THE SRB INTENSITY PROFILES IN THE SC The four intrinsic membrane characteristics of the skin barrier are: (a) the porosity, B, which is the fraction of the skin area occupied by the aqueous pores, (b) the tortuosity, 'T, which is the ratio of the permeant diffusion path length within the skin barrier to the skin barrier thickness, (c) the average pore radius, rpore' 7 and (d) the skin barrier thick­ ness, LlX (2,34-38,40). The goal of the analysis presented here is to obtain quantitative values of the aqueous pore radius, rpore' and of the enhancement in the porosity-to­ tortuosity ratio, BIT, induced by aqueous contacting solutions i, ii, iii, and v-denoted hereafter as the chemical enhancer (E), relative to the aqueous PBS contacting solution iv-denoted hereafter as the control (C). In addition to the visual insights that can be obtained from the TPM skin visualization studies, the analysis presented below can provide quantitative insight on the modification of the skin barrier induced by E relative to C. For example, two modes of perturbation to the aqueous pores are possible: (1) a modification in the average pore radius, rpore' and (2) a modification in the porosity-to­ tortuosity ratio, BIT (2,34-38). The perturbation to the aqueous pores, due to mode 1, is of particular interest for the skin penetration of large irritants present in a skin cleansing formulation, such as surfactant micelles, because a critical average pore radius, rcrit' 8 is required to allow skin penetration of these large permeants (2,3,34). Clearly, as long as rirritant rcrit! where rirritant is the radius of the irritant, then even if (e/T)E(e!T)c, that is, if the enhancement in the porosity-to-tortuosity ratio is greater than unity [E(e!T) 1}, no skin penetration enhancement of the irritant will take place. Conse­ quently, such a formulation should be mild to the skin because the irritant, which could have induced skin barrier perturbation, will not be able to penetrate into the skin. In the Results and Discussion section, we will implement our theoretical framework to quan­ titatively evaluate the aforementioned two modes of perturbation to the aqueous pores induced by E relative to C. Based on the four characteristics of the skin barrier (a-d) (see above), one can express the permeability, Pi, of permeant i (where i corresponds to SRB in the TPM skin visual- 7 Note that rpore is, in fact, an average aqueous pore radius (see Table I) (2,34,35,38,45). In the case of a size distribution of aqueous pore radii, rpore can be considered to be the expectation value of this distribution (2,38). 8 It is noteworthy that the critical average pore radius, rcritJ is a function of the size distribution of aqueous pores in the SC (2,38).

272 JOURNAL OF COSMETIC SCIENCE ization studies reported here) across the SC through the skin aqueous pores as follows (2 ,34,3 5 ,38): Dpore s i p--­ i - TdX (1) where or e is the diffusion coefficient of permeant i in the aqueous pore. Note that D ore can be related to the infinite-dilution diffusion coefficient of permeant i in the bulk aqueous solution, D�, using the following relation (2,34-38): Dpore = D�H(A. .) t t t (2) where H(X.) is the hindrance factor accounting for the hindered diffusion of permeant iJ modeled as a hard sphere of radius, r iJ through the aqueous cylindrical pore, and X. is the ratio of the permeant i radius to the aqueous pore radius, that is, X. i = r/r pore · Anderson and Quinn have defined H(X.) for a spherical permeant i in a cylindrical pore as follows (3 7): H(X.J = cfll - 2.1044X.i + 2.089X.J - 0.948X. ), for X.i =S 0.4 (3) where cpi is the partition coefficient of permeant iJ defined as Cf°re c�, where cf0re is the concentration of permeant i in the pore, and C� is the concentration of permeant i in the bulk solution. Note that equation 3 considers only steric, hard-sphere permeant i-pore wall interactions, and does not account for long-range electrostatic or van der Waals interactions (36,3 7). Using equation 2 in equation 1, one can express the permeability, PiJ as follows: (4) Upon exposing skin to a chemical enhancer, BJ relative to a control, CJ in the context of equation 4, the following relation between the enhancement in the permeability of permeant, iJ (E) p , and the SC average aqueous pore radii values corresponding to E and CJ r 1JOre ,E and r 1J{)re ,o reflected in H(X. ) E and H(X.) c , respectively, is obtained: (E)p =' (P ) ,, = (�)n ( D�E )[ H(X.JE _ ]( dXc ) i (PJc ( � ) D�c H(X.J dXE T C (5) The permeability of permeant i, P , across the SC membrane can also be defined in terms of the flux of permeant i across the membrane (in the z direction) as follows (20,39): (6) where the trans-membrane flux,j i) is predicted by Fick's first law of diffusion, and dC denotes the concentration difference between the donor and the receiver chambers of the