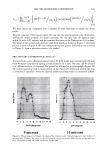
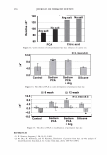
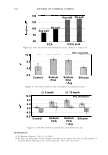
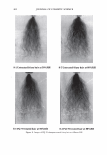
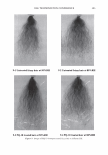
294 JOURNAL OF COSMETIC SCIENCE formation of the finer structure. The phenomenon is explained by the Effective Medium Approximation as super-low refractive index surface. It is considered that light introduction enhances colors of the inside of hair fiber. 4. Obtained structure sizes were about 50 nm in height and 170 nm in lateral space. In such a size range of structure, a light with shorter wavelength was more introduced than with longer one. Surface reflection was shifted to reddish, realizing an angle independent vivid appearance of red dyed hair by the effects of light introduction and reddish surface reflection. ACKNOWLEDGMENTS The authors are grateful to Mr. Dave Muenz, Ms. Bryer Heather, Ms. Weaver Conni, Ms. Christine Hall and Ms. Linda Baird, Kao Brands Company, for technical assistance and helpful discussion. The authors also thank to Dr. Naohisa Kure, Mr. Hiroyuki Saijou and Mr. Satoshi Onitsuka, Kao Corporation, for helpful discussion and guidance. REFERENCES (1) R. F. Stamm, M. L. Garcia and J. J. Fuchs, The optical properties of human hair. Fundamental considerations and goniophotometer curves,]. Soc. Cosmet. Chem., 28, 571-599 (1977). (2) R. F. Stamm, M. L. Garcia and J. J. Fuchs, The optical properties of human hair. The luster of human hair fibers,]. Soc. Cosmet. Chem., 28, 601-609 (1977). (3) F. Wakui, Z. Shinjou, T. Ikeuchi and N. Uchino, Study concerning the luster of human hair,]. Soc. Cosmet. Chem. Jpn., 21(2), 156-161 (1987). (4) S. Nagase, S. Shibuichi, K. Ando, E. Kariya and N. Satoh, Influence of internal structure of hair fiber on hair appearance. I. Light scattering from the porous structure of the medulla of human hair,]. Cosmet. Sci., 53, 89-100 (2002). (5) S. Nagase, N. Satoh and K. Nakamura, Influence of internal structure of hair fiber on hair appearance. II. Consideration of the visual perception mechanism of hair appearance.]. Cosmet. Sci., 5 3, 387-402 (2002). (6) M. Okamoto, R. Yakawa, A. Mamada, S. Inoue, S. Nagase, S. Shibuichi, E. Kariya and N. Satoh, Influence of internal structure of hair fiber on hair appearance. III. Generation of light-scattering factors in hair cuticles and the influence on hair shine,]. Cosmet. Sci., 54, 353-366 (2003). (7) C. G. Bernhard, Structural and functional adaptation in a visual system, Endeavour, 26, 79 (1967). (8) P. B. Clapham and M. C. Hutley, Reduction of lens reflection by the Moth Eye principle, Nature, 244, 281-282 (1973). (9) P. Vukusic and J. R. Sambles, Photonic structures in biology, Nature, 424, 852-855 (2003). (10) J. Springer, A. Poruba and M. Vanecek, Improved three-dimensional optical model for thin-film silicon solar cells,]. Appl. Phys., 96(9), 5329-5337 (2004). (11) J. Springer, B. Rech, W. Reetz, J. Mueller and M. Vanecek, Light trapping and optical losses in microcrystalline silicon pin solar cells deposited on surface-textured glass/ZnO substrates, Sol. Energy Mater. Sol. Cells, 85(1), 1-11 (2005). (12) S. Yamaguchi, Material for deep and vivid color dyeing, SEN'! GAKKAISHI, 40(1-5), .122-324 (1984). (13) T. Sato, N. Nakashima, N. Kyochika and K. Katabe, Shade Enhancement of Textiles, SEN'! GAK- KAISHI, 44(7), 37 (1988). (14) S. Yamaguchi and H. Takanabe, Relation between surface roughness and coloration of silica hybrid polyester fibers, SEN'! GAKKAISHI, 57(4), 126-132 (2001). (15) D. A.G. Bruggeman, Calculation of physical constants of heterogeneous substances, Ann. Phys. (Leipzig), 24, 636 (1935). (16) S. Yoshida and H. Yajima, Optical Thin Films and Devices, University of Tokyo Press, Tokyo, Japan (1994). (17) D. Stroud, The effective medium approximations: Some recent developments, Supperlattices and Mi- crostructures, 23(3), 567-573 (1998).

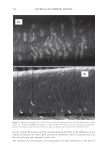
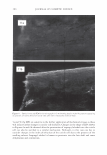
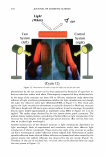
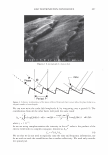
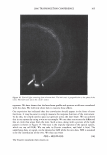
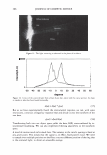
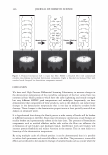
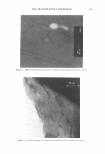
J. Cosmet. Sci., 58, 295-308 Guly/August 2007) Diffraction of light by the cuticle structure of hair HERSCHEL C. BURSTYN and Y ASH K. KAMA TH, TRI/Princeton, 601 Prospect Ave., Princeton, NJ 08542. Synopsis Under a microscope, hair looks like a surface relief grating with an irregular sawtooth profile. Using scalar diffraction theory, we model what has been, until now, assumed to be a specular peak in the light scattering data. Diffraction efficiencies are calculated as a function of cuticle thickness. Convolution with apertures and Gaussian processes yields a picture that is consistent with the observed position and structure of the "specular" peak. When the cuticle thickness fails to satisfy the blaze condition, the scattered light is distributed amongst multiple diffraction orders giving rise to a complex central structure. INTRODUCTION Reflection of light occurs at points where there are discontinuities in the index of refraction. Typically these occur at interfaces with air. In hair this region occurs at the surface of the cuticle (small shingles that cover the hair shaft). This observation has been used to quantify hair luster. The models that have been used to interpret the data have been based upon geometrical optics. The rake angle of the cuticle relative to the longitudinal axis of the hair, -y, is measured by determining the "scattering angle" twice: first with the hair oriented from root to tip, and then from tip to root. The difference in these two directions is equal to four times the rake angle (as the deviation from the "expected direction" in each case is twice the rake angle). The geometrical optic inter- pretation of the rake angle is demonstrated in Figure 1. If one models the hair as a grating, the angles into which diffraction occurs are fixed by the periodicity. This model is motivated by micrographs of which Figure 2 is one example. However, the energy that appears in any given order will depend upon the grating depth. It is this shift in the energy distribution that yields a perceived shift in the angle of "specular" reflection. It also explains why the specular assumption yields a rake angle estimator that can be a few tenths of a degree in error. This can be shown using scalar diffraction theory. The redistribution of energy amongst the diffraction orders, also expresses itself as changes in the shape of the peak, something that has been ignored to date. THEORY We start with the development of the grating equation (1). Only at specific angles does the light reflected off the facet surfaces add coherently. This can be seen in the Figure 3. 295