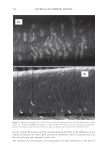
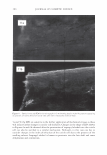
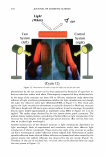
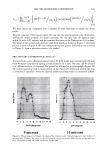
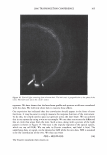
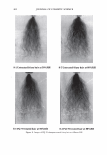
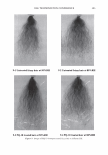
300 JOURNAL OF COSMETIC SCIENCE The beam's radius Tl, goes as where ( ( z ) 2 )1/ 2 Tj(z) = 1lo 1 + ZR is the Rayleigh range. The wavefront curvature propagates as (9) The Rayleigh range is that distance over which the beam does not significantly diverge. Notice that the beam is a plane wave both at focus and at infinity. If our detector is well within the Raleigh range we can simplify the expression to (86) For a beam with a waist of 1 mm = 1000 µm, the Rayleigh range of the order of 5 meters (@0.63 µm). If focused to 100 microns this reduces to 4.9 cm. This distribution is centered upon a diffraction order which is located at 0 0 . As such, r = z(0 - 0 0 ). We can define Tj 0 /z as D and rewrite the expression as [ (0 - 0o)2 ] [ ( ( z ) ) ] E(r,z) = Eo exp - n2 exp - j kz - ZR (8c) Thus we can also interpret the spatial distribution as an angular one. The propagating phase part is nominally a plane wave that will have almost no effect on the final observed intensity. The observed intensity in the plane of the detector, for a single order, will be a Gaussian distributed in angle about a direction that is specified by the grating equation. GRATING PERIOD VARIABILITY CAN BE MODELED AS A GAUSSIAN PHASE SCREEN We modeled the hair as a phase grating of specific period. The cuticles, as they wear, will thin and fracture. We have shown how the depth can be accounted for in a scalar diffraction theory. We need to somehow account for the increased variability in the pitch. There is however a local modulation of period. A random modulation can be accounted for by introducing a Gaussian phase screen as a transmission mask. Because the screen acts multiplicatively in real space, it appears as a convolution in the transform space (3 ). In other words the Gaussian profile that is the laser's beam cross-section is convoluted with phase screen's Gaussian in angle space, resulting in what may be referred to as an excess spreading about the mean (angular) position. This is explicitly expressed in the following way.

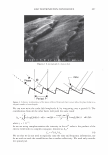
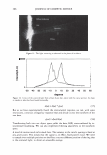
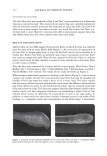
2006 TRI/PRINCETON CONFERENCE Given two Gaussian distributions, p 1 (x ) =- 2 1 exp[- (x - µ ) 2 ], 1TCJ 1 2CJ 1 pi (x ) = __exp[- 2 (x - µ ) 2 ]' 1TCJ 2 2CJ 2 their convolution is another Gaussian of broader variance and 301 (11) In our case the mean of the process is zero. The randomness of the grating that is the hair is noticed as an excess spreading of the laser beam. CONVOLVING THE BROADENED DIFFRACTED ORDERS WITH THE DETECTOR APERTURE Measurement systems have finite apertures. We can assume that this aperture is a slit of angular width 20, centered about and angle, a. For any given order, the detector sees a portion of the curve under the Gaussian intensity distribution as shown in Figure 6. This leads to a sum of error functions (ERF). a-8 a+8 a-8 a µ a µ I I I\ ) \ µ a+8 a+8 µa-8 Figure 6. The integral under the Gaussian can come in as a sum or difference of error functions depending upon the position of the aperture center relative to the location of the mean, and the aperture width.