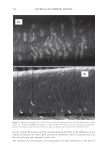
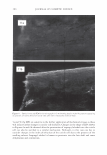
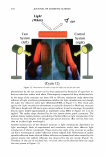
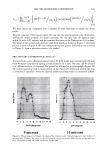
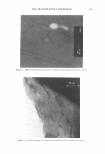
2006 TRI/PRINCETON CONFERENCE 297 Figure 2. A micrograph of a human hair. I '◄ ►' I Period, P I Figure 3. Coherent reinforcement of the waves reflected from each facet occurs when the phase delay is an integral number of wavelengths. We can now write the scalar field amplitude A, by integrating over a period (2). The contributions from all the other facets will yield the same result p p 1 f r exp(-jwt ) f Am = rA exp[j(cp(x) - nKx - wt)]dx = p A exp[j(cp(x) - nKx)]dx. 0 0 where j = (-1) 112 • As we are using complex notation the intensity in the mth order is the product of the electric field with its complex conjugate, denoted as Am * I - 2 IA *A m - r m m· (4) We see that we do not need to explicitly carry the time and frequency information, nor do we wish to track the overall factor due to surface reflectivity. We need only consider the spatial part

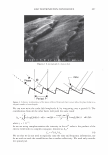
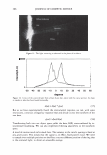
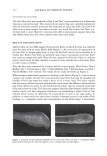
298 JOURNAL OF COSMETIC SCIENCE Um = �I exp[j(cf(x) - nKx)]dx. (5) We evaluate U m using our phase function. The round-trip phase shift due to depth is 0 at x = 0, and maximum (2a) at x P. It is also linear. Substituting explicitly into equation 5 yields: p p Um = H exp[j(2et(x/p)- nKx)]dx = H exp[j(et - m1r): ]dx (6) 0 0 2( 1 ) {exp[j2(u - m,r)]-1 }. u - m1T Multiplying by the complex conjugate yields the intensity 1 1 U*mum = {1 - cos2(a - m1r)} = 2 {1 - cos(2a)} (7) 2(a - m,r)2 2(a - m,r) 1 . 2 = sm (a). (u - m,r)2 We show a plot of this function for the significant orders in Figure 4. The relative intensities of the various orders at a specific depth are shown in Figure 5. 1 � 0.9 -� 0.8 - "iii 0.7 e o.6 i 0.5 -I--:-=-�-:--:,-������...........,_----+-.......,_�� � 0.4 - -� 0.3 S 0.2 --t--'----.----:-'¼-���--�---,.....:.......�--=--� C Q .1 -·I-----''-:--------""'--�.,,,..,._-.--�.-�� 0 __ .1,,,aii��!!lilllli,..�==ir,::��:.,,c,,;.iiii,,aa..-;.;,�;..ilii 0 0.2 0.4 0.6 0.8 1 depth (microns) - - order a - - - - order 1 -order-1 -order2 - - - order 3 -order-3 --order4 Figure 4. The relative amplitude of the various orders as a function of a.. For a reasonable hair a. = 10 should correspond to a depth of about 1 micron. Notice that different orders peak at different depths and that at specific depths all the light is contained in a single order. This is the basis of blazing. Almost no light is found in negative orders.