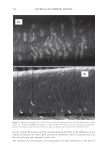
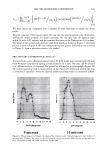
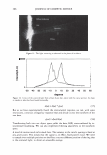
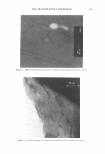
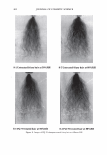
2006 TRI/PRINCETON CONFERENCE 305 Figure 10. Conical light scattering from a human hair. The hair's axis is perpendicular to the plane of the circle. The hair's axis pieces the circle's center. exposure. We have shown that the laser beam profile and aperture width are convoluted with the data. We will now show how to remove these effects. Our exposition has indicated that the convolution should appear in the form of error functions. It may be easier to simply measure the response function of the instrument. To do this, we simply need to pass our aperture across the laser beam. We can achieve this in our system by using a wire as our sample. We can thus scan across the diffracted line or circle that arises from the wire. Such a trace, along with a picture of the light pattern is shown in Figure 14. The trace is the impulse response of the optical system, which we can call H(0). We can take its Fourier transform, and label it h(w). The underlying data, or signal, can be denoted as G(0) while the raw data, D(0) is assumed to be the convolution of the two. We thus can write D(0) = H(0) Q9 G(0). (16) The Fourier transform then results in:

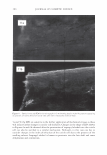
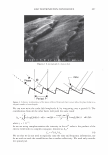
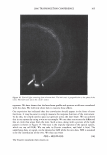
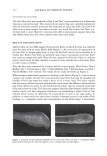
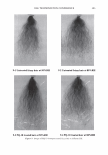
306 - :::i � b · C C JOURNAL OF COSMETIC SCIENCE Figure 11. The light scattering as observed in the plane of incidence. -50 -40 -30 -20 -10 0 10 20 30 40 50 60 degrees Figure 12. A trace of the scattered light from a black Asian hair, taken with the coarse aperture. Its shape is similar to what has been found historically. d(w) = h(w) * g(w) (17) But as we have experimentally found the instrumental response, we can, with some restrictions, construct a frequency response h(w) and divide it into the transform of the raw data. g(w) = d(w)lh(w) (18) Transforming back into our object space yields the data, G(8), unencumbered by in- strumental broadening. We can also implement filtering algorithms in the transform space. A word of caution needs to be made here. The variance in the cuticle spacing is fixed at any given point. This means that the signal is, in effect, fixed pattern noise. We need to sample over multiple positions on the fiber, or across different position of the ring that is the scattered light, to obtain an ensemble average.